A Quick Review of Powers, Exponents and Scientific Notation
=== by Bob Sutherland ===
A quick review of the basic terminology and symbols used to represent powers, exponents, square roots, cube roots and scientific notation.
Powers and Exponents in Mathematics
In Junior High School your Mathematics teacher called them powers. In Senior High School your Mathematics teacher changed their name to exponents. In high school Mathematics classrooms powers and exponents are two different words meaning the same thing.
In 53 the base number is 5 and the power or exponent is 3. The exponent tells you how many times to multiply the base number by itself.
Some Mathematics and Computer Science textbooks call the base number a radix.
51 = 5
52 = 5 x 5 = 25
53 = 5 x 5 x 5 = 125
54 = 5 x 5 x 5 x 5 = 625
Any base number having an exponent of zero is equal to one.
Therefore 1 = 20 = 30 = 40 = 50 = 60 and so on.
An exponent of 1/2 means to find the square root of the number.
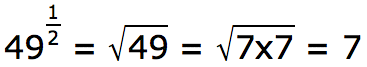
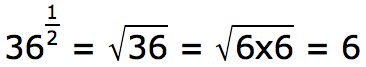
An exponent of 1/3 means to find the cube root of the number.
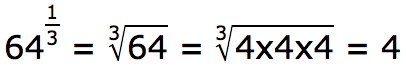

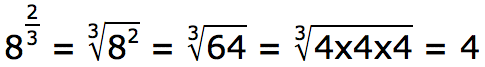
A negative exponent means you have a fraction with one as the numerator.
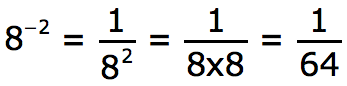
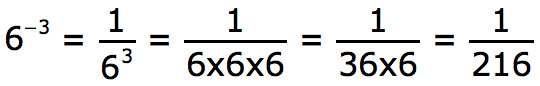
Exponents on a Computer
In the early years of computers the only software that was generally available were computer programming languages. When using a computer programming language all characters had to be typed as plain letters and numbers on a single line. It was not possible to type a small exponent up beside the top right corner of a larger base number.
To try to solve this problem and other problems regarding trying to type mathematical symbols and notation on a computer the early inventors of computer programming languages came up with a number of alternative solutions. Since the computer programming languages they were inventing were in competition with each other for acceptance by computer programmers you cannot expect the inventors to have reached any sort of agreement among themselves as to how to represent exponents when typing. One solution that some of them used, which seems to have some logic to it, was to type a caret ^ preceding an exponent. This notation is still around and being used by people today. Although not known and recognized by everyone it is what I would recommend you use when you cannot type little superscripts for exponents beside a larger base number.
Fortunately the inventors of the computer programming languages did much better at reaching an agreement to use the asterisk * as a multiplication sign and a forward slash / as a division sign on a computer. The ÷ symbol used for division in Mathematics classrooms was not available as a key on the computer keyboard. Using the letter x key for both a multiplication sign and for the letter x could lead to confusion, especially for students taking high school Mathematics where the letters x and y are often used as variables in equations and formulas.
Here are some examples:
7 * 3 = 21
12 / 4 = 3
6^1 = 6
6^2 = 6 * 6 = 36
6^3 = 6 * 6 * 6 = 216
6^4 = 6 * 6 * 6 * 6 = 1296
25^(0.5) = 25^(1/2) = (5 * 5)^(1/2) = 5
121^(0.5) = 121^(1/2) = (11 * 11)^(1/2) = 11
81^(0.25) = 81^(1/4) = (9 * 9)^(1/4) = (3 * 3 * 3 * 3)^(1/4) = 3
2^-5 = 1/(2^5) = 1/(2 * 2 * 2 * 2 * 2) = 1/32
7^-2 = 1/(7^2) = 1/(7*7) = 1/49
Hint: You will need to use brackets quite frequently when typing math equations on a single line to avoid any ambiguity in meaning.
Scientific Notation
Scientific Notation is an alternative method for writing very wide numbers that have many digits either before or after the decimal point. For example, when measuring distances out in space between planets and stars we may want to use scientific notation.
Scientific notation numbers are written as a number between one and ten multiplied by ten to a power.
The power of ten is easy to find because it is simply how many places you have to move the decimal point over to put the decimal point after the first digit.
Here are some examples of converting a number to scientific notation:
39485.72 = 3.948572 x 104
0.0000261 = 2.61 x 10-5
0.000000000082700394 = 8.2700394 x 10-11
Average distance from Neptune to the sun in Kilometres:
4497000000 = 4.497 x 109
Scientific Notation on a Computer
When a number has too many digits for a computer to to be able to store the number in its memory or display the number on its screen the computer will convert the number to scientific notation. Numbers displayed in scientific notation should be regarded as rounded off numbers.
In scientific notation on a computer the number will be typed on a single line with all of the characters the same size and no spaces. There will be a decimal point after the first digit. The letter e for exponent will replace the x 10 used in regular scientific notation. The exponent will consist of a plus or minus sign followed by a number.
| Scientific Notation | Scientific Notation on a Computer |
|---|---|
| 5.683 x 108 | 5.683e+8 |
| 1.928445 x 10-15 | 1.928445e-15 |
| 9.9937 x 10-34 | 9.9937e-34 |
| 1.0001 x 1024 | 1.0001e+24 |

